扫码获取更多资源

●顺序表的操作实现

定位操作

算法设计

（1）从顺序表的第一个数据元素起，依次与给定的数据元素值进行比较，如果存在与其 值相等的数据元素，则返回第一个相等元素的位序；

（2）如果查遍整个顺序表都没有找到与其值相等的数据元素，则返回为0

算法描述

算法分析

（1）问题规模：线性表的“当前长度”（设值为n）。

（2）基本操作：指示位置的变量加l（i+ + ）。

（3）时间分析：当i = l时，变量i加1操作的次数为0;当i = n时，变量i加1操作的次 数为n-1；定位成功时的平均执行次数为（n—1）/2,定位不成功时的执行次数为n,因此算 法2-6的时间复杂度为O（n）。

插入操作

线性表的插入操作是指在线性表的第i-1个数据元素和第i个数据元素之间插入一个 新的数据元素，也就是使长度为n的线性表（a】,a?,处，a—i , ai,a”）变成长度为n+1 的线性表,数据元素ai_1和之间的逻辑关系发生了变化。 在线性表的顺序存储结构中，由于逻辑上相邻的数据元素在物理位置上也是相邻的，因此除 非i = n+l,否则必须移动数据元素才能反映这个逻辑关系的变化。

时间分析

如果当前存储空间已满，则算法的时间主要花费在增加空间（Increment （L））±，此时需 要腾挪原空间中的数据到新空间newlist中，移动次数为n0

如果当前存储空间不满，则算法的时间主要花费在for循环中后移元素的次数上。当 i = n+l时,后移数据元素次数为0,即算法在最优时的时间复杂度是0（1）;当i=l时，后 移数据元素次数为no

删除操作

线性表的删除操作是使长度为n的线性表（a】日2 ,a3,a—i斗，ai+1• ,an）变成长度 为n— 1的线性表（a】形挪3,…,a—】,ai+1• ,an）,数据元素a—i和ai+1之间的逻辑关系发 生了变化。

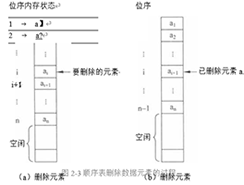
一般情况下，在删除顺序表的第i个数据元素时，需要将第i + 1至第n个（共n-i）数据 元素依次向前移动一个位置。

（1）检查删除操作要求的有关参数的合理性，如果不合理，则给出错误信息。

（2）将待删除数据元素的值赋给变量。

（3）把顺序表中原来第i+1至第n个数据元素依次向前移一个位置。

（4）修正顺序表的长度。

联系我们：