扫码获取更多资源

●简单的模式匹配方法——BF算法

这是一种带回溯的匹配算法，简称BF(Brute-Force,布鲁特-福斯)算法，其基本思想是： 从主串S第pos个字符开始和模式T第一个字符进行比较，如果相等，则继续比较两者的 后续字符；否则，从主串S的下一个字符开始和模式T的第一个字符进行比较，重复上述过 程。如果T中的字符全部比较完毕，则说明本趟匹配成功；否则说明匹配失败。

●BF算法设计

在主串S和模式T中设置比较的下标i和j(初始时，i = pos,j = l)；循环比较直到S中 所剩字符个数小于T的长度或T的所有字符均比较完：如果= 则继续比较S和 T的下一个字符；否则，将i和j回溯，准备下一趟比较。如果T中的所有字符均比较完，则 说明匹配成功，返回匹配的起始比较下标；否则，说明匹配失败，返回0。

例如：主串S=nababcabcacbab\模式T=Habcac%从主串S的第一个字符开始匹配。 模式匹配过程如图4-7所示。

BF算法分析

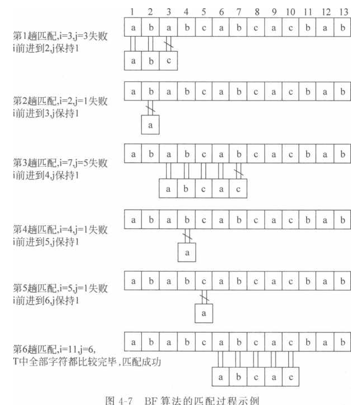
设主串S长度为n,模式T长度为mo算法4-20在匹配成功的情况下有两种极端 情况。

在最好的情况下，每趟不成功的匹配都发生在模式T的第一个字符。 例如，S=”aaaaaaaaaabc”，T=”bc”，从主串S的第一个字符开始匹配。假设匹配成功 发生在$处，那么在第i-1趟不成功的匹配中共比较了 i—1次，第i趟成功的匹配共比较 了 m次，则总共比较了 i-1 + m次；由于所有匹配成功的可能共有n —m +1种，设从$开 始与模式T匹配成功的概率为P”在等概率情况下，pi = l/(n—m+1),因此平均的比较次

KMP算法分析

设主串S长度为n,模式T长度为mo StrIndex_KMP函数在任何情况下的时间复杂 度均为O(n+m)； Get_next函数的时间复杂度为O(m),但通常模式的长度比主串的长度 要小得多，因此对整个匹配算法4-21来说,增加的这点时间是值得的。

KMP算法仅当模式与主串存在许多“部分匹配”情况下才显得比BF算法快得多。虽 然BF算法的时间复杂度为O(nXm),但在一般情况下其实际执行时间近似于()(n+m), 因此至今仍被广泛釆用。KMP算法最大的特点是指示主串的指针不需要回溯，对主串仅 需要从头至尾扫描一遍即可完成匹配，因此对于处理外设输入的庞大数据文件非常有效，可 以边读入边匹配，而不需要回头重读。

联系我们：