扫码获取更多资源

二叉树的存储表示及操作实现

●二叉树的重要性质

性质1在二叉树的第i层上至多有个结点(i'l)。证明：利用数学归纳法证明。

归纳基础:i=l时，只有一个根结点，显然2i=2】T=2° = l,所以命题成立。

归纳假设：假设对所有的j（lMjVi）命题成立，即第j层上至多有2宀 个结点，证明j = i 时，命题也成立。

归纳步骤：根据归纳假设，第i-1层上至多有2_2个结点，由于二叉树的每个结点至 多有两个孩子，因此第i层上的结点数至多是第i-1层上最大结点数的2倍。即j = i时，该 层上至多有2X2-2=21个结点，故命题成立。

性质2深度为k的二叉树至多有2k-l个结点（k>l）0

证明：在具有相同深度的二叉树中，仅当每一层上都含有最大结点数时，其树中的结点 数最多。因此利用性质1可得，深度为k的二叉树的结点数至多为：

性质3对任何一棵二叉树T,如果其叶结点数为no,度为2的结点数为电，则：r）o=n2+l0 证明：因为二叉树中所有结点的度均小于或等于2,所以结点总数（记为n）应该等于度 为0的结点数、度为1的结点数（记为山）和度为2的结点数之和，由式（6-1）表示：

n = n0 + rij + n2

性质4具有n个结点的完全二叉树的深度为Uog2nJ+l0

证明：假设具有n个结点的完全二叉树的深度为k,根据完全二叉树的定义和性质2

性质5对一棵具有n个结点的完全二叉树中的结点从1开始按层序编号，则对于任 意的编号为i(lWiWn)的结点(简称为结点i),有：

(1)如果i>l,则结点i的双亲编号为Li/2 J；否则结点i是根结点，无双亲；

(2)如果2i《n,则结点i的左孩子编号为2i；否则结点i无左孩子，且该结点为叶结点；

(3)如果2i+l

证明：因为可以从(2)和(3)推出(1),所以先证明(2)和(3)。

对于i = l,结点i就是根结点，因此无双亲。由完全二叉树的定义，其左孩子应该是结 点2,右孩子应该是结点3O如果2>n,即不存在结点2,则此结点i无左孩子，且为叶结点； 如果3>n,即不存在结点3,则结点i无右孩子。

对于i>l,可以分为下面两种情况讨论：

情况1

设第j(l^j^[_log2nj )层第一个结点编号为i, 由二叉树性质2可知，i = 2,7，那么结点i的左孩子 必定为第j + 1层的第一个结点，其编号为2，= 2X (2j-l)=2i；右孩子必定为第j + 1层的第二个结 点，编号为2i+l。如果2i〉n,则结点i无左孩子， 且为叶结点；如果2i+l>n,则结点i无右孩子，如 图6-23所示。

情况2

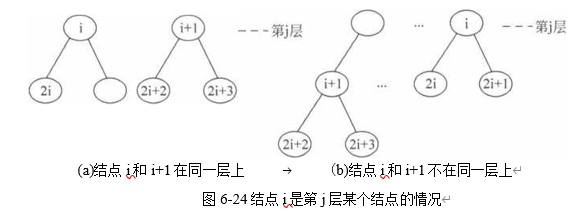
设第j(lWjW|Jog2n」)层上某个结点编号为i(2j~1n,则结点i+1无左孩子,且为叶结点；如果2(i+l) + l>n,则结点i+1无右孩子，如图6-24所示。

由(2)和(3)推出(1):当i>l时，如果结点i为左孩子，即2X (i/2) = i,则i/2是结点i的双 亲；如果结点i为右孩子，则i=2p+l,即结点i的双亲应该为p,而p=(i—l)/2= Li/2 Jo 故命题成立。

联系我们：

微信