扫码获取更多资源

●二叉树的存储表示及操作实现

二叉树的存储结构除了要求能存储各结点的数据信息，还要求能唯一地反映二叉树中 各结点之间的逻辑关系，即双亲与孩子之间的关系。和其他数据结构一样，二叉树也分为顺 序存储结构和链式存储结构。

归纳基础:i=l时，只有一个根结点，显然2i=2】T=2° = l,所以命题成立。

二叉树顺序表的定义

对于一般二叉树，增添“虚结点”，使之“转化”为一棵完全二叉树；以一组连续空间按层 序存储二叉树中所有的“实结点”和“虚结点”。釆用这种存储结构的二叉树称为二叉树顺序 表(BiTree Sequential List) o

图6-25(a)给出了一棵二叉树，图6-25(b)给出了增设“虚结点”之后“转化”的完全二叉 树，图6-25(c)给岀了二叉树顺序表结构。用“①”表示“虚结点”，即不存在此结点。

二叉树顺序表的特点

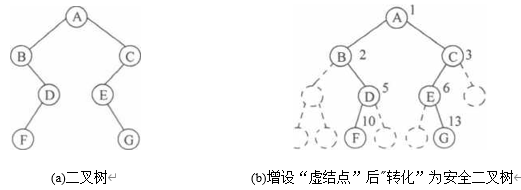
二叉树顺序表会造成存储空间的浪费，最坏的情况是如图6-26所示的右斜树。一棵深 度为k的右斜树，只有k个结点，却需要分配2k-l个存储单元。事实上，二叉树顺序表仅 适合存储完全二叉树。

性质2深度为k的二叉树至多有2k-l个结点（k>l）0

在二叉树顺序表中进行插入和删除操作时，需要移动结点；当元素个数较多、元素信息 量较大时，移动元素所花费的时间相当多。事实上，二叉树顺序表一般仅适合存储完全二叉 树；对于一般二叉树来说，可以选择下面介绍的二叉链表。

性质3对任何一棵二叉树T,如果其叶结点数为no,度为2的结点数为电，则：r）o=n2+l0 证明：因为二叉树中所有结点的度均小于或等于2,所以结点总数（记为n）应该等于度 为0的结点数、度为1的结点数（记为山）和度为2的结点数之和，由式（6-1）表示：

二叉链表的特点

n = n0 + rij + n2

一个二叉链表由根指针T唯一确定。如果二叉树为空，则T=NUI丄；如果结点的某 个孩子不存在，则相应的指针为空。具有n个结点的二叉链表中，共有2n个指针域。其中 只有n-1个用来指示结点的左孩子和右孩子，其余的n+1个指针域为空。

证明：假设具有n个结点的完全二叉树的深度为k,根据完全二叉树的定义和性质2

在二叉链表中，从某结点出发可以直接访问到它的 孩子，但要找到其双亲则需要从根结点开始搜索，最坏情 况下需要遍历整个二叉链表。为了便于找到结点的双 亲，可以在二叉链表的结点结构中再增加一个指向其双亲的指针域parent,其结点结构如 图6-29所示。釆用这种存储结构的二叉树称为二叉树的三叉链表（TriTree Linked List）。

(1)如果i>l,则结点i的双亲编号为Li/2 J；否则结点i是根结点，无双亲；

先序遍历二叉树顺序表

一棵n个结点的完全二叉树以顺序表作为存储结构，采用非递归方法按先序遍历并输 出所有结点的数据信息，有下面四种情况： ①如果当前结点是根结点，则令其编号j=l; ②如果当前结点的左孩子存在，则修改当前结点编号j = 2Xj； ③如果当前结点的左孩子不存在，但右兄弟存在，则修改当前结点编号j=j + l; ④如果当前结点的左孩子及右兄弟均不存在，但其双亲之右兄弟存在，则修改当前结 点编号j=j/2 + l。

联系我们：