扫码获取更多资源

●邻接矩阵的定义

图的邻接矩阵存储也称数组表示法。用一个一维数组存储图中顶点的信息，一个二维 数组存储图中边(或弧)的信息(即各顶点之间的邻接关系)，该二维数组称为图的邻接矩阵 (Adjacency Matrix) o

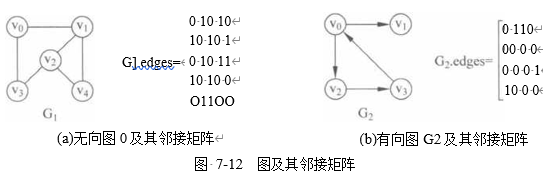
图7-12(a)所示的是无向图G1及其邻接矩阵G】.edges,图7-12(b)所示的是有向图G2 及其邻接矩阵G2. edges 0显然，无向图(网)的邻接矩阵一定是对称矩阵。

邻接矩阵的类型定义

说明：VRTyp e是顶点关系类型。对无权图，用1或0表示相邻或不相邻,VRType可 以定义为值是0和1的枚举类型；对有权图,VRType可以定义为权值类型。

求顶点的邻接点

对于n个顶点的图，先通过LocateVex（G, v）找到顶点v在G中的位置，即v在顶点数 组vexs中的序号i;再在邻接矩阵edges中寻找第i行上第一个值为“1”的分量，其对应的 列号j即为v的第一个邻接点在图中的位置。同理，下一个邻接点在图中的位置便为j列之 后第一个值为“1”的分量所在列号。

存储空间

如果图中有n个顶点，则邻接矩阵表示法需要存放n个顶点和n2个边（或弧）信息的存 储量，其空间复杂度S（n） = O（n2）o如果考虑无向图的邻接矩阵是对称的，则可以釆用压 缩存储的方式，即只需要存入邻接矩阵的下三角（或上三角）元素。

邻接表的定义

图的邻接表存储类似于树的孩子链表表示法。对于图中每个顶点V,建立一个链表，第 i个链表中的结点表示依附于V]的边（对有向图是以Vj为尾的弧）。每个链表上附设一个表 头结点，为了随机访问任一顶点的链表，这些表头结点通常以顺序结构方式存储。采用这种 存储结构的图称为邻接表（Adjacency List） o

如果图中有n个顶点，则邻接矩阵表示法需要存放n个顶点和n2个边（或弧）信息的存 储量，其空间复杂度S（n） = O（n2）o如果考虑无向图的邻接矩阵是对称的，则可以釆用压 缩存储的方式，即只需要存入邻接矩阵的下三角（或上三角）元素。

在邻接表存储结构中存在两种结点：头结点和表结点，如图7-14所示。其中，头结点 由两个域组成，顶点域（vex）存放顶点信息，指针域（firstedge）指向第一条依附于该顶点的 边（或弧）；表结点由三个域组成，邻接点域（adivex）指示与头结点相邻接的顶点在图中的位 置，链域（nextedge）指向与头结点相邻接的下一条边（或弧）；权域（weight）存放网中边（或 弧）的权值（图无此域）。

联系我们：