扫码获取更多资源

●树的类型定义

树(Tree)是n(n2。)个结点的有限集合。当n = 0时，称为空树；任意一棵非空树满足 以下两个条件：

2、数据元素：数据元素是数据的基本单位，但不是最小单位。在程序中通常作为一个整体来进行考虑和处理，又称为记录。

(1)有且仅有一个特定的称为根(Root)的结点；

(2)当n>l时，除根结点之外的其余结点被分成m(m>0)个互不相交的有限集合T】, T2,其中每个集合又是一棵树，并称为这个根结点的子树(Subtree)。

显然，树的定义是递归的，即在树的定义中又用到了树的概念。树的递归定义刻画了树 的固有特性：一棵非空树是由根结点及若干棵子树构成的，而子树又可以由其根结点和若 干棵更小的子树构成。

5、数据类型：数据类型是一个值的集合和定义在此集合上的一组操作的总称。1）原子类型。其值不可再分的数据类型（整型 int 、字符型 char )2）结构类型。其值可以再分解为若干成分（分量）的数据类型．

例如，图6-2(a)是一棵具有9个结点的树，T={A, B, C,…，H, I},结点A为树T的 根，其余结点分为两个互不相交的集合：T】 = {B, D, E, F, 1)和T? = {C, G, H},Tt和T? 构成了根结点A的两棵子树。子树卩的根为B,其余结点分为三个互不相交的集合：TH = {D},T12 = {E, 1}和T】3 = {F},TU、T】2和「3构成了子树T|根结点B的三棵子树。子树 T2的根为C,其余结点分为两个

以及对数据对象的基本操作的集合。

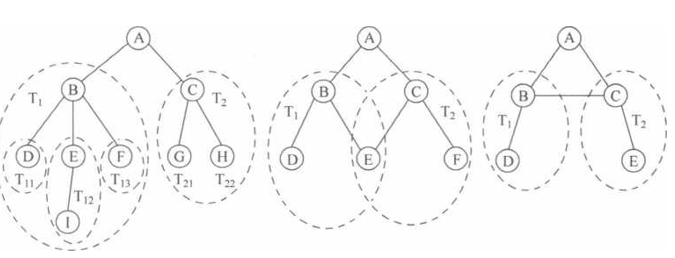
互不相交的集合：T21 = {G}和T22 = {H},T2］和T22构成 了子树T2根结点C的两棵子树。以此类推，直到每棵子树只有一个根结点为止。互不相交的集合：T21 = {G}和T22 = {H},T2］和T22构成 了子树T2根结点C的两棵子树。以此类推，直到每棵子树只有一个根结点为止。

抽象数据类型的形式定义用以下三元组表示：

树的表示形式

树有四种表示形式，如图6-5所示。

(1)树形图：用结点和分支来描述树的结构，是树形结构的主要表示方法。

(2)嵌套图：用集合的包含关系来描述树的结构。

(3)凹入表：类似于书目录的形式来描述树的结构。

(4)广义表：用广义表的形式来描述树的结构。根作为由子树森林组成的表的名字写 在表的左边。

树的表示形式的多样化正说明了树结构在日常生活中以及计算机程序设计中的重要 性。一般来说，分等级的分类方案都可以使用层次结构来表示，即都可以形成一个树结构。

上一页||下一页

联系我们：