扫码获取更多资源

●树与二叉树的转换

树中每个结点最多只有一个最左边的孩子(第一个孩子)和一个右邻的兄弟。按照这种 关系很自然地就能将树转换成二叉树，且转换是唯一的；或者将一棵缺少右子树的二叉树 还原为树，且还原是唯一的。

但是，当釆用二叉链表存储二叉树时，只能找到结点的左孩子和右孩子信息，而不能直 接得到结点在某一序列中的前驱和后继信息，这种信息只有在遍历二叉树的动态过程才能 得到，其时间复杂度为()(n)(设二叉树结点个数为n)o如果将这些信息在首次遍历时获得 后就保存起来，则可以在“需要”时直接获得结点的前驱和后继信息。

树转换为二叉树

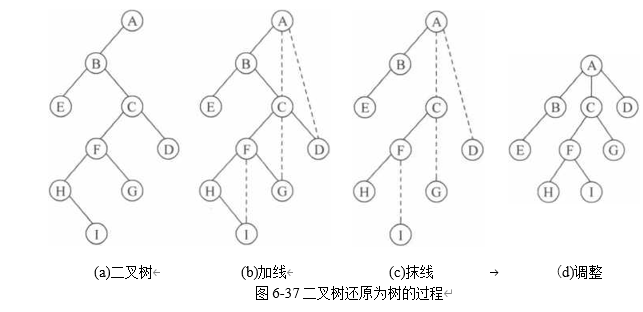
将一棵树转换为二叉树的方法是：

(1)加线：在树中所有相邻兄弟结点之间加一条连线，将其隐含的“兄-弟”关系以及 “父-右子”关系显著表示出来，如图6-36(b)所示。

(2)抹线：对树中的每个结点，只保留它与其最左边的孩子，即第一个孩子结点之间的 连线，抹掉与其他孩子结点之间的连线，即抹去其“父-右子”关系，如图6-36(c)所示。

(3)调整：以树根结点作为二叉树根结点，将树根与其最左边的孩子，即第一个孩子之 间的“父-子”关系改为“父-左子”关系，且将各结点按照二叉树的层次排列，形成二叉树的结 构，如图6-36(d)所示。

可以看岀，二叉树中左分支上的各结点在原来的树中是“父-第一个孩子”关系，而右分 支上的各结点在原来的树中是兄弟关系。由于树的根结点没有兄弟，所以转换之后，二叉树 的根结点的右子树必为空。

二叉树还原为树

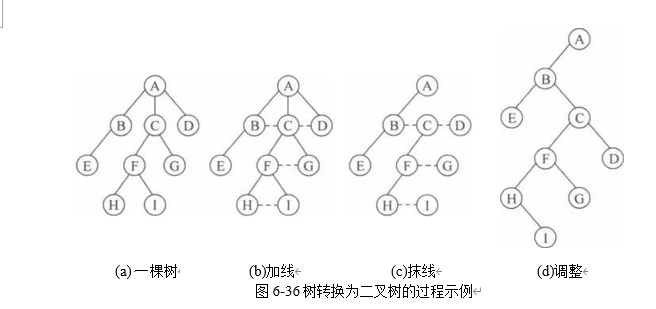
将一棵缺少右子树的二叉树还原为树的方法是： (1) 加线：在二叉树中所有结点双亲与该结点右链上的每个结点之间加一连线，以“父- 子”关系显著表示岀来，如图6-37(b)所示。

联系我们：