扫码获取更多资源

●树和二叉树习题

填空题

1.有一棵二叉树如图6-48所示：这棵树的根结点是（ ），这棵树的叶子结点是（

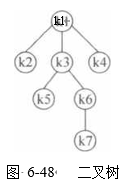
结点k3的度是（ ），这棵树的度是（ ），这棵树的树高是（

结点k3的孩子是（ ），结点k3的父亲是（ ）。

2.深度为k的完全二叉树，至少包括（ ）个结点，至多包括（ ） 个结点；如果具有n个结点的完全二叉树按照层序从1开始编号，则 编号最小的叶子结点序号是（ ）。

3.一棵二叉树的第i（i21）层最多有（ ）个结点；一棵有n（n>0）

个结点的满二叉树共有（ ）个叶子结点和（ ）个非终端结点。

4.某二叉树的先序遍历序列是ABCDEFG,中序遍历序列是

CBDAFGE,则其后序遍历序列是（ ）。

5.在具有n个结点的二叉链表中，共有（ ）个指针域，其中（

向其左右孩子，剩下的（ ）个指针域则是空的。

填空题

1.已知一棵度为m的树中有：n】个度为1的结点个度为2的结点，……,nm个度 为m的结点，那么该树中共有多少个叶子结点？

2.一个深度为h的满k叉树有如下性质：第h层上的结点都是叶子结点，其余各层上 每个结点都有k棵非空子树。按层次顺序（同层自左至右）从1开始对全部结点编号。

（1）各层的结点数目是多少？

（2编号为i的结点的双亲结点（若存在）的编号是多少？

（3编号为i的结点的第j个孩子结点（若存在）的编号是多少？

（4编号为i的结点的有右兄弟的条件是什么？其右兄弟的编号是多少？

3.试找岀分别满足下面条件的所有二叉树：

（1）先序序列和中序序列相同。

（2）中序序列和后序序列相同。

（3）先序序列和后序序列相同。

（4）先序、中序、后序序列均相同。

4.如果二叉树中各结点的值均不相同，则由二叉树的先序序列和中序序列，或由其中 序序列和后序序列均能唯一确定一棵二叉树，但由先序序列和后序序列却不一定能唯一确 定一棵二叉树。

（1）已知一棵二叉树的先序序列和中序序列分别为ABDGHCEFI和GDHBAECIF,试 画出此二叉树。

（2）已知一棵二叉树的中序序列和后序序列分别为BDCEAFHG和DECBHGFA,试 画出此二叉树。

（3）已知一棵二叉树的先序序列和后序序列分别为AB和BA,请画出这两棵不同的二 叉树。

5.一个二叉树顺序表如图6-49所示，试画出该二叉树的二叉链表。

联系我们：