扫码获取更多资源

●二叉树

二叉树是一种重要的树形结构，许多实际问题抽象出来的数据结构往往是二叉树的形 式。二叉树也是一种最简单的树结构，其存储结构更具有规范性和确定性，算法也较为简 单，特别适合计算机处理，而且任何树都可以简单地转换为二叉树。

双亲表示法

二叉树的类型定义

二叉树(Binary Tree)是n(n20)个结点的有限集合。当n = 0时，称为空二叉树；任意 一棵非空树满足以下两个条件：

(1)有且仅有一个特定的称为根(Root)的结点；

(2)当n>l时，除根结点之外的其余结点最多分成两个互不相交的有限集合，其中每 个集合又是一棵树，并称为这个根结点的左子树和右子树。

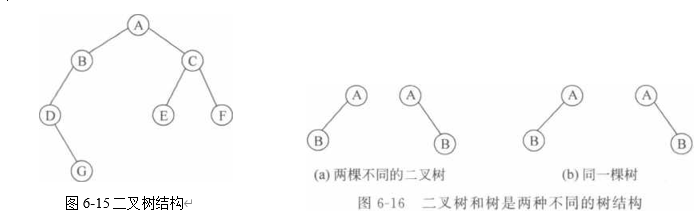
显然，二叉树的定义是递归的。图6-15所示的是一个二叉树。

由二叉树的定义，可以得到二叉树的两个特点：其一，每个结点最多有两棵子树，因此 二叉树中不存在度大于2的结点。其二，二叉树是有序的，其次序不能任意颠倒，即使树中 的某个结点只有一棵子树，也要区分它是左子树还是右子树，因此二叉树和树是两种不同的 树结构，如图6-16所示。

二叉树的基本形态

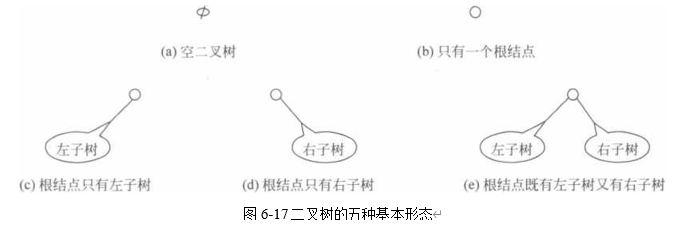
二叉树的递归定义表明：二叉树或是为空，或是只有一个根结点，或是一个根结点加上 左子树，或是一个根结点加上右子树，或是一个根结点加上左子树和右子树。由此，二叉树 可以有五种基本形态，如图6-17所示。

二叉树的遍历

先序遍历

先序遍历的定义是如果二叉树为空，则空操作返回；否则： ①问根结点； ②先序遍历根结点的左子树； ③先序遍历根结点的右子树。 例如，对于图6-15所示的二叉树，按先序遍历得到的结点序列为：A B D G C E F。

中序遍历

中序遍历的定义是如果二叉树为空，则空操作返回；否则： ①中序遍历根结点的左子树； ②访问根结点； ③中序遍历根结点的右子树。 例如，对于图6-15所示的二叉树，按中序遍历得到的结点序列为：D G B A E C F。

后序遍历

后序遍历的定义是如果二叉树为空，则空操作返回；否则： ①后序遍历根结点的左子树； ②后序遍历根结点的右子树； ③访问根结点。

联系我们：