扫码获取更多资源

●线索二叉树

遍历二叉树就是按照一定的规律将二叉树中的结点排列成一个线性序列，得到其先序 序列，或中序序列，或后序序列。这实质上是对一个非线性结构进行线性化操作，使每个结 点(除了开始结点和终端结点)有且仅有一个前驱和后继。

但是，当釆用二叉链表存储二叉树时，只能找到结点的左孩子和右孩子信息，而不能直 接得到结点在某一序列中的前驱和后继信息，这种信息只有在遍历二叉树的动态过程才能 得到，其时间复杂度为()(n)(设二叉树结点个数为n)o如果将这些信息在首次遍历时获得 后就保存起来，则可以在“需要”时直接获得结点的前驱和后继信息。

二叉树顺序表的定义

对于一般二叉树，增添“虚结点”，使之“转化”为一棵完全二叉树；以一组连续空间按层 序存储二叉树中所有的“实结点”和“虚结点”。釆用这种存储结构的二叉树称为二叉树顺序 表(BiTree Sequential List) o

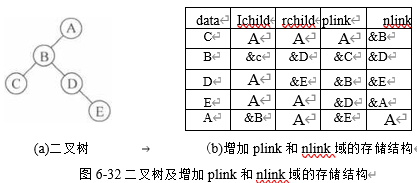
那么，应该如何保存遍历二叉树动态过程中所获得的某一结点前驱和后继信息呢？方 案有两个。 (1) 为了方便求某一结点的前驱和后继，可以在原有二叉链表的结点结构中增加两个 链域：plink和nlink，分别指向结点在任意次序遍历时获得的前驱和后继。对图6-32(a)给 出的二叉树，按照中序遍历，每个结点链域值如图6-32(b)所示。

(2) 因为在清n个结点的二叉树中，有n+1个空链域，所以可以利用这些空链域来存 放结点的前驱和后继信息。

显然，第一种方案非常浪费空间，不但没有利用二叉链表中原有的空链域，还要多增加 两个链域。而第二种方案利用了二叉链表中原有空链域，提高了结构存储密度，是一种较实 用的做法,本书采用这个方案。

线索链表的定义

如果结点有左孩子，则可令其左指针域Ichild指示其左孩子，否则指示其前驱；如果结 点有右孩子，则令其右指针域rchild指示其右孩子，否则指示其后继。为了避免混淆，需要 改变二叉链表的结点结构，即每个结点增设两个标志位Itag和rtago采用这种存储结构的 二叉树称为线索链表(Threaded Linked List) o

线索链表的操作实现

对于在中序线索链表上的任一结点P，其前驱有以下三种情况：

①如果p->lchild = Thrt(头结点)，则无前驱，给出相应错误信息；

②如果p->ltag = Thread,则其左指针所指向的结点便是其前驱；

③如果p->ltag=Link,则根据中序遍历操作定义，其前驱应是遍历其左子树时最后 一个访问的结点，即左子树中的最右下结点。因此只需要沿着其左孩子的右指针向下查找， 当某结点的右标志为Thread时，即为所要寻找的前驱。

联系我们：