扫码获取更多资源

●图习题

填空题

1.已知一个无向图用邻接矩阵表示，第i个顶点的度是（ ）;已知一个有向图用邻 接矩阵表示，第i个顶点的度是（ ）。

2.设无向图G1中顶点数为n,那么G1至少有（ ）条边，至多有（ ）条边；设有 向图G2中顶点数为n,那么图G2至少有（ ）条弧，至多有（ ）条弧。

3.图的深度优先遍历类似于树的（ ）遍历，它所用到的数据结构是（ ）;图的广 度优先遍历类似于树的（ ）遍历，它所用到的数据结构是（ ）o

4.对于含有n个顶点和e条边的连通图，如果利用普里姆算法求最小生成树，则时间 复杂度为（ ）;如果利用克鲁斯卡尔算法求最小生成树，则时间复杂度为（ ）。

5.如果一个有向图不存在（ ），则该图的全部顶点可以排列成一个拓扑序列。

问答题

1.个顶点的无向图，如果釆用邻接矩阵存储，则：

（1） 如何计算图中有多少条边？ （2） 如何判断任意两个顶点i和j是否有边相连？ （3） 如何求解任意一个顶点的度是多少？

2.n个顶点的无向图，如果釆用邻接表存储，则：

（1） 如何计算图中有多少条边？ （2） 如何判断任意两个顶点i和j是否有边相连？ （3） 如何求解任意一个顶点的度是多少？

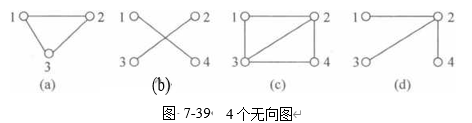
3.在图7-39所示的4个无向图中：

（1） 找出所有的简单环； （2） 判断哪些图是连通图？对非连通图给出其连通分量； （3） 判断哪些图是无环连通图（又称自由树），或无环非连通图（又称自由森林）？

4.在图7-40所示的有向图中：

（1）判断该图是强连通图吗？如果不是，则给出其强连通分量； （2） 找出所有的简单路径及简单回路； （3） 计算每个顶点的度、入度和出度。

5.在图7-41所示的连通图中：

（1） 画出其邻接矩阵和邻接表； （2） 如果从顶点V。出发对该图进行遍历，分别给出一个按深度优先遍历和广度优先遍 历的顶点序列。

算法设计题

1.试设计一个算法：对一个以邻接表表示的含有n个顶点和e条弧的有向图G,求解 其每个顶点的度。

2.试设计一个算法：输出无向图G中从顶点v_到V的长度为length的所有简单 路径。

3.试设计一个算法：将一个无向图的邻接矩阵转换为邻接表。

4.试设计一个算法：基于深度优先遍历算法，判断以邻接表存储的有向图中是否存在 由顶点Vi到Vj的路径(i^j) O

5.试设计一个算法：判断无向图G是否连通；如果连通，则返回1；否则返回0。

联系我们：