扫码获取更多资源

●有向无环图及其应用

一个无环的有向图称为有向无环图(Directed Acyclic Graph),简称DAG图。DAG图 是一类比有向树更一般的特殊有向图，图7-27给出了有向树、DAG图和有向图的示例。

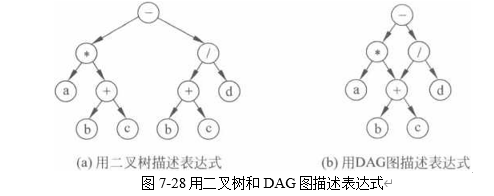
DAG图是描述公共关系表达式的有效工具。例如有表达式(a * (b+c)) —((b+c)/d)，可 以用二叉树表示，如图7-28(a)所示；也可以用DAG图表示，如图7-28(b)所示。不难发现, 表达式中相同的子式在二叉树中会重复岀现，而在DAG图中则可以实现共享，从而节省了 空间。

生成树和生成森林

DAG图也是描述一项工程或系统进程过程的有效工具。通常，把计划安排、施工过程、 生产流程、软件工程等都当成一个工程，除了最简单的情况之外，几乎所有的工程都可以分 为若干个称作活动(Activity)的子工程，而这些活动之间，通常受着一定条件的约束，例如其 中某些活动必须在另一些活动完成之后才能开始。对整个工程和系统，人们常常会关心以 下的两个问题：

(1)工程能否顺利进行？

(2)整个工程完成必需的最短时间是多少？

这就是求拓扑排序(Topological Sort)和关键路径(Critical Path)的问题。求解有向图 的拓扑排序和关键路径是很有实际应用价值的问题。

拓扑排序

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，该有向 图称为顶点表示活动的网，简称AOV网(Activity On Vertex Network) o

AOV网中的弧表示活动之间存在的某种制约关系。例如，计算机软件专业的学生必 须学习一系列规定课程，那么学生应该按照怎样的顺序来学习这些课程呢？可以把这个问 题看成是一个工程，其活动就是学习每一门课程。例如高等数学是独立于其他课程的基础课；而有些课程却需 要有先修课程，例如学完程序设计语言和离散数学后才能学习数据结构。先修课程规定了 课程之间的优先关系，这种优先关系可以用图7-29(b)所示的AOV网表示，其中顶点表示 课程，弧表示课程之间的优先关系。

在AOV网中，不应该出现有向环，因为存在环就意味着某项活动应该以自己为先决条 件，显然，这是不可能的。如果设计出这样的流程图，工程便无法进行；而对程序的数据流 图来说，则表明存在一个死循环。因此，对给定的AOV网应该首先判定网中是否存在环。 测试的方法就是对AOV网进行拓扑排序。

1.拓扑排序的定义

设G=(V, VR)是一个具有n个顶点的有向图，V中的顶点序列｛vi，v2,…，v”｝称为 一个拓扑序列(Topological Order),当且仅当满足下列条件:如果从顶点«到顶点巧有一 条路径，则在顶点序列中巧必在Vj之前。对一个有向图构造拓扑序列的过程称为拓扑排序 (Topological Sort) 0

联系我们：