扫码获取更多资源

●广义表

广义表，又称为列表(Lists,釆用复数形式是为了与统称的表List的区别)，是线性表的 一种推广和扩充，即在广义表中取消了对线性表元素的原子限制，允许它们具有其自身的结 构；广义表又区别于数组，即不要求每个元素具有相同类型。

●广义表的类型定义

广义表(Generalized List)是n(n}0)个元素的有限序列,一般记作： LS = (a】，a2,…，an)

三元组顺序表的定义

将表示稀疏矩阵非零元素的三元组按行优先顺序排列，并依次存放在一组地址连续的 存储单元里的方式称为稀疏矩阵的顺序存储结构，釆用这种存储结构的稀疏矩阵称为三元 组顺序表(Triple Sequential List) o

其中：LS是广义表的名称；为(iMiMn)是LS的成员(也称为直接元素)，它可以是单个元 素，也可以是一个广义表，分别称为LS的原子和子表。一般用大写字母表示广义表，用小 写字母表示原子。

当广义表LS非空时，第一个直接元素称为LS的表头(Head)；广义表LS中除去表头 后其余的直接元素组成的广义表称为LS的表尾(Tail)。广义表LS中的直接元素个数称 为LS的长度；广义表LS中括号的最大嵌套层数称为LS的深度。

广义表的图形表示

可以采用图形方法表示广义表的逻辑结构：对每个广义表元素公用一个结点来表示， 如果街为原子，则用矩形结点表示；如果街为广义表，则用圆形结点表示；结点之间的边表 示元素之间的“包含/属于”关系。对于上面列举的6个广义表，其图形表示如图5-19所示。

广义表的主要特性

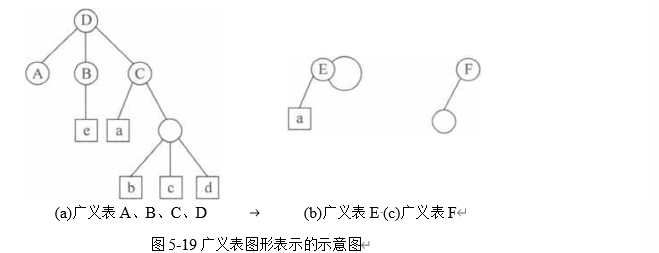
从上述广义表的定义和例子可以看岀，广义表具有以下四个特性：

(1)广义线性性：对任意广义表来说，如果不考虑其元素的内部结构，则它是一个线性 表，它的直接元素之间是线性关系。

(2)元素复合性：广义表中的元素有原子和子表两种，因此，广义表中元素的类型不统 一。一个子表，在某一层上被当作元素，但就它本身的结构而言，也是广义表。在其他数据 结构中，并不把子表这样的复合元素看作元素。

(3)元素递归性：广义表可以是递归的。广义表的定义并没有限制元素的递归，即广 义表也可以是其自身的子表，这种递归性使得广义表具有较强的表达能力。

(4)元素共享性：广义表以及广义表的元素可以为其他广义表所共享。例如，对于上 面列举的6个广义表，广义表A、广义表B、广义表C是广义表D的共享子表。 广义表的上述四个特性对于它的使用价值和应用效果起到了很大的作用。广义表的结 构相当灵活，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。例如，当二维数 组的每行(或每列)作为子表处理时，二维数组即为一个广义表；如果限制广义表中元素的 共享和递归，广义表和树对应；如果限制广义表的递归并允许元素共享，则广义表和图 对应。

联系我们：