扫码获取更多资源

●无向图的连通分量

在对无向图进行遍历时，对于连通图，仅需要从图中任一顶点出发，进行深度优先搜索 或广度优先搜索，便可以访问到图中所有的顶点。对于非连通图，则需要从多个顶点出发进 行搜索，而每一次从一个新的起点出发进行搜索过程中得到的顶点访问序列恰好是一个连 通分量中的顶点集。

算法设计

要想判定一个无向图是否为连通图，或有几个连通分量，可以设置一个计数器count, 初始时取值为0,每调用一次遍历算法，就使count增加1。这样，当对整个图的搜索结束 时，依据count的值，就可以确定图的连通性，或者有几个连通分量。

算法描述

算法分析

对于有n个顶点和e条边的图G,算法7-5的时间复杂度为O(n+c)。

生成树和生成森林

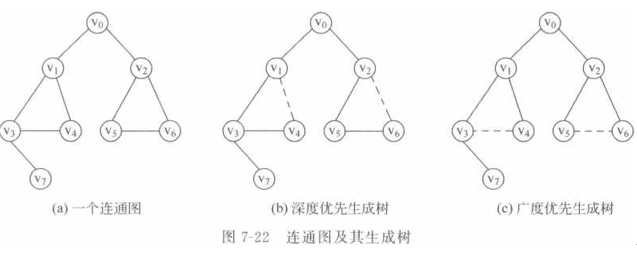
从连通图G=(V, VR)中的任一顶点出发进行遍历，必定将边集VR(G)分成两个集合 TE(G)和BE(G),其中TE(G)是遍历过程中经历的边的集合,BE(G)是剩余的边的集合。 显然,TE(G)和G中所有顶点一起构成了 G的极小连通子图，它是G的一棵生成树。由深 度优先搜索得到的为深度优先生成树，由广度优先搜索得到的为广度优先生成树。

对于非连通图，每个连通分量中的顶点集和搜索时走过的边一起构成了若干棵生成树, 这些连通分量的生成树组成了非连通图的生成森林。由深度优先搜索得到的为深度优先生

成森林，由广度优先搜索得到的为广度优先生成森林。

图7-22(b)和图7-22(c)给出的是图7-22(a)所示连通图的深度优先生成树和广度优先 生成树，图中实线为集合TE(G)中的边，虚线为集合BE(G)中的边。

联系我们：